[ Maths 3ème ] Factorisation, identités remarquables

Publié le 8 février 2011 par Prof

I. Développement (révisions)

Définition :

Développer un produit, c'est le transformer en une somme ou une différence.

Propriétés :

Pour tous nombres a, b, c, d et k, on a :

produit		somme ou différence
k(a + b)	=	ka + kb
k(a - b)	=	ka - kb
(a + b)(c + d)	=	ac + ad + bc + bd

Exemple : Développer l'expression A = $4(2x + 1) + (3x - 1)(4x + 5)$ .
A = $4(2x + 1)$ + $\red (3x - 1)(4x + 5)$
A = $4 \times 2x + 4 \times 1$ + $\red 3x \times 4x + 3x \times 5 - 1 \times 4x - 1 \times 5$
$\text{A} = 8x + 4 + 12x^2 + 15x - 4x - 5\\ \text{A} = 12x^2 + 19x - 1$

II. Identités remarquables

1. Carré d'une somme

Propriété :

Pour tous nombres a et b, on a : (a + b)² = a² + 2ab + b²

Démontrons ce résultat :
par le calcul, en utilisant la double distributivité :
(a + b)² = (a + b)(a + b) = a × a + a × b + b × a + b × b = a² + ab + ab + b² = a² + 2ab + b²

en utilisant la géométrie :
Lorsque a et b sont deux nombres positifs, on peut établir l'égalité en considérant la figure ci-dessous :
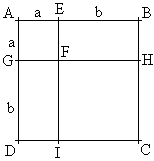
factorisation, développement, identités remarquables - troisième : image 1
ABCD est un carré de côté a + b, AEFG est un carré de côté a, FHCI est un carré de côté b, EBHF et GFID sont deux rectangles de largeur a et de longueur b.
Exprimons de deux manières différentes l'aire $\mathcal{A}$ du carré ABCD :
ABCD est un carré de côté a + b, donc $\mathcal{A}$ = (a + b)²

ou :
$\mathcal{A} = \mathcal{A}_{\text{AEFG}} + \mathcal{A}_{\text{EBHF}} + \mathcal{A}_{\text{FHCI}} + \mathcal{A}_{\text{GFID}}$
$\mathcal{A}$ = a² + a × b + b² + a × b
$\mathcal{A}$ = a² + 2ab + b²
D'où : (a + b)² = a² + 2ab + b²

Exemples :

Développer :
$(x + 5)^2 = x^2 + 2 \times x \times 5 + 5^2 = x^2 + 10x + 25\\ (5x + 3)^2 = (5x)^2 + 2 \times 5x \times 3 + 3^2 = 25x^2 + 30x + 9\\ (2x + 1)^2 = (2x)^2 + 2 \times 2x \times 1 + 1^2 = 4x^2 + 4x + 1$

Calculer :
11² = (10 + 1)² = 10² + 2 × 10 × 1 + 1² = 100 + 20 + 1 = 121
13² = (10 + 3)² = 10² + 2 × 10 × 3 + 3² = 100 + 60 + 9 = 169
22² = (20 + 2)² = 20² + 2 × 20 × 2 + 2² = 400 + 80 + 4 = 484
101² = (100 + 1)² = 100² + 2 × 100 × 1 + 1² = 10 000 + 200 + 1 = 10 201

2. Carré d'une différence

Propriété :

Pour tous nombres a et b, on a : (a - b)² = a² - 2ab + b²

Démontrons ce résultat :
par le calcul, en utilisant la double distributivité :
(a - b)² = (a - b)(a - b) = a × a - a × b - b × a + b × b = a² - ab - ab + b² = a² - 2ab + b²

en utilisant la géométrie :
Lorsque a et b sont deux nombres positifs, on peut établir l'égalité en considérant la figure ci-dessous :
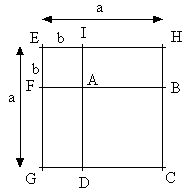
factorisation, développement, identités remarquables - troisième : image 2
EHCG est un carré de côté a, EIAF est un carré de côté b, ABCD est un carré de côté (a - b) et IHBA et ADGF sont deux rectangles de largeur b et de longueur (a - b).
Exprimons de deux manières différentes l'aire $\mathcal{A}$ du carré ABCD :
ABCD est un carré de côté a - b, donc $\mathcal{A}$ = (a - b)²
ou :
$\mathcal{A} = \mathcal{A}_{\text{EHCG}} - \mathcal{A}_{\text{EIAF}} - \mathcal{A}_{\text{IHBA}} - \mathcal{A}_{\text{ADGF}}$
$\mathcal{A}$ = a² - b² - b × (a - b) - b × (a - b)
$\mathcal{A}$ = a² - b² - ba + b² - ba + b²
$\mathcal{A}$ = a² - 2ab + b²
D'où : (a - b)² = a² - 2ab + b²

Exemples :
Développer :
$(x - 7)^2 = x^2 - 2 \times x \times 7 + 7^2 = x^2 - 14x + 49\\ (2x - 3)^2 = (2x)^2 - 2 \times 2x \times 3 + 3^2 = 4x^2 - 12x + 9\\ (5x - 3)^2 = (5x)^2 - 2 \times 5x \times 3 + 3^2 = 25x^2 - 30x + 9$

Calculer :
99² = (100 - 1)² = 100² - 2 × 100 × 1 + 1² = 10 000 - 200 + 1 = 9 801

3. Produit d'une différence par une somme

Propriété :

Pour tous nombres a et b, on a : (a - b)(a + b) = a² - b²

Démontrons ce résultat :
par le calcul, en utilisant la double distributivité :
(a - b)(a + b) = a × a + a × b - b × a - b × b = a² - b²

en utilisant la géométrie :
Lorsque a et b sont deux nombres positifs, on peut établir l'égalité en considérant la figure ci-dessous :
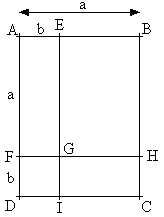
factorisation, développement, identités remarquables - troisième : image 3
ABCD est un rectangle de longueur (a + b) et de largeur a, AEGF est un rectangle de largeur b et de longueur a, GHCI est un rectangle de longueur (a - b) et de largeur b et FGID est un carré de côté b.
Exprimons de deux manières différentes l'aire $\mathcal{A}$ du rectangle EBCI :
EBCI est un un rectangle de longueur (a + b) et de largeur (a - b), donc $\mathcal{A}$ = (a - b)(a + b)
ou :
$\mathcal{A} = \mathcal{A}_{\text{ABCD}} - \mathcal{A}_{\text{AEGF}} - \mathcal{A}_{\text{FGID}}$
$\mathcal{A}$ = a(a + b) - ba - b²
$\mathcal{A}$ = a² + ab - ab - b²
$\mathcal{A}$ = a² - b²
D'où : (a - b)(a + b) = a² - b²

Exemples :
Développer :
$(x - 3)(x + 3) = x^2 - 3^2 = x^2 - 9\\ (5x - 3)(5x + 3) = (5x)^2 - 3^2 = 25x^2 - 9\\ (2x + 5)(2x - 5) = (2x)^2 - 5^2 = 4x^2 - 25$

Calculer :
99 × 101 = (100 - 1)(100 + 1) = 100² - 1² = 10 000 - 1 = 9 999
21 × 19 = (20 + 1)(20 - 1) = 20² - 1² = 400 - 1 = 399
32 × 28 = (30 + 2)(30 - 2) = 30² - 2² = 900 - 4 = 896

III. Factorisation

Définition :

Factoriser une somme ou une différence, c'est la transformer en un produit.

1. Reconnaître un facteur commun

Exemples : Factorisons les expressions suivantes :
$\text{B} = (x - 1)(x + 2) + (x - 1)(x + 3) \hspace{40pt} (x - 1)$ est le facteur commun
$\text{B} = \boxed{(x - 1)}(x + 2) + \boxed{(x - 1)}(x + 3)\\ \text{B} = (x - 1)[(x + 2) + (x + 3)]\\ \text{B} = (x - 1)(x + 2 + x + 3)\\ \text{B} = (x - 1)(2x + 5)$

$\text{C} = (5x + 3)(2x - 1) - (5x + 3)^2 \hspace{40pt} (5x + 3)$ est le facteur commun
$\text{C} = \boxed{(5x + 3)}(2x - 1) - \boxed{(5x + 3)}(5x + 3)\\ \text{C} = (5x + 3)[(2x - 1) - (5x + 3)]\\ \text{C} = (5x + 3)(2x - 1 - 5x - 3)\\ \text{C} = (5x + 3)(-3x - 4)$

$\text{D} = (7x + 6)(3x - 5) - (3x - 5) \hspace{40pt} (3x - 5)$ est le facteur commun
$\text{D} = (7x + 6)\boxed{(3x - 5)} - \boxed{(3x - 5)} \times 1\\ \text{D} = (3x - 5)[(7x + 6) - 1]\\ \text{D} = (3x - 5)(7x + 6 - 1)\\ \text{D} = (3x - 5)(7x + 5)$

2. Reconnaître une identité remarquable

Exemples : Factorisons les expressions suivantes :
$\text{E} = x^2 + 10x + 25$
$\text{E} = x^2 + 2 \times x \times 5 + 5^2$ de la forme a² + 2 × a × b + b², avec a = $x$ et b = 5, donc :
$\text{E} = (x + 5)^2$

$\text{F} = 4x^2 - 28x + 49$
$\text{F} = (2x)^2 - 2 \times 2x \times 7 + 7^2$
F est de la forme a² - 2 × a × b + b², avec a = $2x$ et b = 7, donc :
$\text{F} = (2x - 7)^2$

$\text{G} = x^2 - 36$
$\text{G} = x^2 - 6^2$ de la forme a² - b², avec a = $x$ et b = 6, donc :
$\text{G} = (x - 6)(x + 6)$

$\text{H} = (4x + 3)^2 - (7x - 1)^2$ de la forme a² - b² avec a = $4x + 3$ et b = $7x - 1$
$\text{H} = [(4x + 3) - (7x - 1)][(4x + 3) + (7x - 1)]\\ \text{H} = (4x + 3 - 7x + 1)(4x + 3 + 7x - 1)\\ \text{H} = (-3x + 4)(11x + 2)$

(source:ilemaths)